- Le nombre pi
- Article sur agm
- Programme naïf
- Liens
- Le nombre sqrt(2)
- Article sur un algorithme naïf
- Programme naïf
- Liens
- Les fractales en théorie
- Article sur l'ensemble de Mandelbrot
- Liens
- Les fractales en couleurs
- Galerie Mandelbrot/Julia
- Galerie Attracteurs
- Galerie IFS
- Galerie Bassins
- Commentaires
- tutorial Qifs
- Programme fracat
- Programme Qifs
- Bibliographie
- Liens
- 01 02
- Les automates cellulaires
- Mes premières images
- Mon petit cluster
- Les résultats...
- Calculatrice kal (en mode console)
- Programme
- Voyage scolaire
- Barcelone avril 2006
- GNU/Linux
- CM nFORCE2
- Sur l'auteur...
- mon CV
Ecrivez-moi :
raphael dot pasquier at free dot fr
Mise à jour le 2 octobre 2006
Méthode élémentaire utilisant un développement limité
Quelques égalités
En utilisant les égalités sur la racine carré
![]() ,
,
![]() ,
,
![]() pour des nombres positifs
pour des nombres positifs ![]() et
et ![]() , on vérifie facilement
les quelques formules suivantes sur
, on vérifie facilement
les quelques formules suivantes sur ![]() :
:
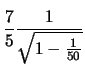 |
|||
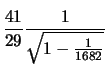 |
|||
| et encore | |||
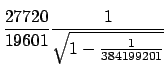 |
|||
| et enfin pour | |||
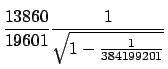 |
Un peu d'analyse
Les égalités précédentes surEn effet au voisinage de 0, on peut décomposer la fonction
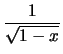 |
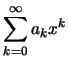 |
||
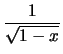 |
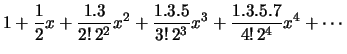 |
c'est-à-dire avec
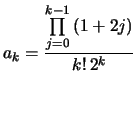
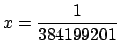
Algorithme élémentaire
Rappel rapide sur les flottants à virgule fixe
Pour comprendre tout l'intérêt des algorithmes proposés, un détour doit être fait sur une méthode pour représenter les "réels" dans les ordinateurs, et qu'on appelle flottants à virgule fixe.Pour la clarté de l'exposé je vais raisonner sur un représentation en base 10 mais n'importe quel base convient. En particulier pour l'implémentation en langage C, l'auteur a utlisé la base
Cette représentaion repose sur le simple fait que tout nombre décimale n'ayant que
De plus l'addition et la soustraction entre nombres décimales à
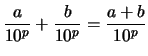
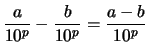
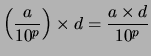
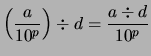
Par exemple dans cette représentaion, si on travaille avec ![]() chiffres après la virgule, le réel
chiffres après la virgule, le réel
![]() avec
avec ![]() zéros correspond à l'entier
zéros correspond à l'entier
![]() avec
avec ![]() zéros.
zéros.
Pour une explication plus détaillée, je vous renvoie à la page de mon site sur la représentation des
nombres.
Ainsi pour calculer ![]() avec une précision à
avec une précision à ![]() près (avec
près (avec ![]() par exemple),
on est ramené à faire des additions, des soustractions sur des entiers de grande taille
(de l'ordre de
par exemple),
on est ramené à faire des additions, des soustractions sur des entiers de grande taille
(de l'ordre de ![]() ) et des multiplications, divisions par de "petits" entiers
( en général inférieur à dix millions) comme nous allons le voir dans le prochain paragraphe.
) et des multiplications, divisions par de "petits" entiers
( en général inférieur à dix millions) comme nous allons le voir dans le prochain paragraphe.
Algorithme utilisant un développement en série entière
En posant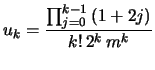
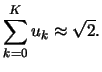
Le nombre
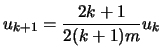
| répéter | |
|
|
(1) |
|
|
(2) |
|
|
(3) |
|
|
(4) |
|
|
|
| jusqu'à |
|
|
|
(5) |
|
|
(6) |
| afficher
|
Remarques :
- Comme on peut le voir sur l'algorithme précédent, on fait des additions et soustractions sur de
grands entiers (lignes (3) et (4)) des divisions par de petits entiers (lignes (1), (2) et (6))
et une multiplication par un petit entier (ligne (5)).
Pour la ligne (2), on divise bien par un petit entier car pour calculer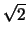 avec
avec 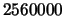 chiffres après la virgule par exemple,
chiffres après la virgule par exemple, 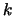 varie entre 0 et
varie entre 0 et
 et plus généralement pour avoir
et plus généralement pour avoir 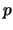 chiffres après la virgule, il faut prendre
chiffres après la virgule, il faut prendre
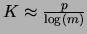 qui est un entier petit pour des valeurs de
qui est un entier petit pour des valeurs de 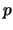 inférieures à
inférieures à
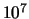 (valeurs courantes en pratique).
(valeurs courantes en pratique).
- J'ai choisi la deuxième égalité pour
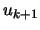 car il est plus facile de faire deux divisions
avec de petits diviseurs que de faire une multiplication puis une division par des entiers
qui dépasseraient la taille d'un chiffre dans la base que j'ai choisi ( cad
car il est plus facile de faire deux divisions
avec de petits diviseurs que de faire une multiplication puis une division par des entiers
qui dépasseraient la taille d'un chiffre dans la base que j'ai choisi ( cad 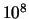 dans mon cas).
dans mon cas).
- L'algorithme a un comportement asymptotique de l'ordre de
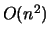 : i.e. pour doubler le nombre
de décimales exactes, il faut multiplier par
: i.e. pour doubler le nombre
de décimales exactes, il faut multiplier par 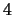 le temps de calcul.
le temps de calcul.
- Puisque
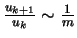 et
et
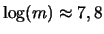 , on gagne
asymptotiquement
, on gagne
asymptotiquement 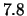 chiffres par itération ( ce qui explique la "lenteur" relative de
l'algorithme).
chiffres par itération ( ce qui explique la "lenteur" relative de
l'algorithme).
Résultats :
- Voici le temps mis par le programme de l'auteur :
nombre de décimales exactes 5 000 10 000 100 000 1 000 000 2 560 000 durée du calcul en secondes 0.08 0.3 28.7 3375.4 22680.1 - Configuration :
- Processeur : Athlon K7 700 Mhz.
- Carte mère : ASUS K7M supportant 256 Mo de SDRAM à 100 Mhz.
- Système d'exploitation : Mandrake8.2.
- Compilateur : gcc-3.0.4.
- En pratique :
- Pour compiler le programme, tapez dans une console (dans le répertoire contenant le source) :
gmake - Pour exécuter le programme :
./pii sqrt2 10
sqrt2 10
où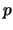 est le nombre de décimales justes désirées.
est le nombre de décimales justes désirées.
- Pour compiler le programme, tapez dans une console (dans le répertoire contenant le source) :
About this document ...
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 1 info_sqrt2.tex
The translation was initiated by raphi on 2004-05-30