- Le nombre pi
- Article sur agm
- Programme naïf
- Liens
- Le nombre sqrt(2)
- Article sur un algorithme naïf
- Programme naïf
- Liens
- Les fractales en théorie
- Article sur l'ensemble de Mandelbrot
- Liens
- Les fractales en couleurs
- Galerie Mandelbrot/Julia
- Galerie Attracteurs
- Galerie IFS
- Galerie Bassins
- Commentaires
- tutorial Qifs
- Programme fracat
- Programme Qifs
- Bibliographie
- Liens
- 01 02
- Les automates cellulaires
- Mes premières images
- Mon petit cluster
- Les résultats...
- Calculatrice kal (en mode console)
- Programme
- Voyage scolaire
- Barcelone avril 2006
- GNU/Linux
- CM nFORCE2
- Sur l'auteur...
- mon CV
Ecrivez-moi :
raphael dot pasquier at free dot fr
Mise à jour le 2 octobre 2006
Cette page provient du site
http://www.pi314.net/ .
En fait l'auteur propose aux internautes de refaire des démonstrations ce que je fis et
je propose sur cette page mon travail.
Ainsi j'invite l'internaute à suivre les démonstrations et à les refaire :)
Introduction
Le mathématicien Gauss introduisit et étudia les suites moyennes arithmético-géométriques ainsi définies par récurrence :
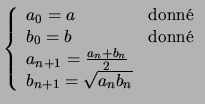
Cette convergence est précisément quadratique.
Autrement dit le nombre de chiffres exactes à la limite double à chaque itérations.
Voici un exemple avec
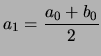 |
|||
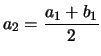 |
|||
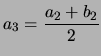 |
|||
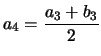 |
|||
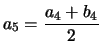 |
|||
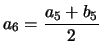 |
|||
Mais Quel lien y a-t-il avec le nombre
En définissant la fonction ![]() par
par
![]() on montre que cette fonction est
continue sur
on montre que cette fonction est
continue sur
![]() et
dérivable sur
et
dérivable sur
![]() et
surtout la relation :
et
surtout la relation :
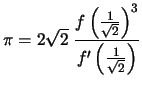
Algorithme de Salamin/Brent (1976)
alors
![$\displaystyle U_n = \frac{4a_n^2}{1-2 \sum\limits_{k=1}^{n}{2^k (a_k^2 - b_k^2 )}}
\xrightarrow[n \to \infty]{} \pi
$](images/pi_agm/img42.png)
Algorithmes des frères Borwein (1984)
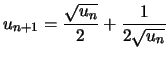
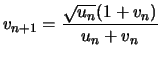
![$\displaystyle p_{n+1} = p_n u_n \frac{1+u_n}{1+v_n} \xrightarrow[n \to \infty]{} \pi
$](images/pi_agm/img48.png)
Encore les frères Borwein (1987)
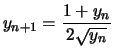
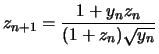
![$\displaystyle f_{n+1} = f_n \frac{1+y_n}{1+z_n} \xrightarrow[n \to \infty]{} \pi
$](images/pi_agm/img54.png)
Les suites moyennes arithmético-géométriques
Définition
Soient deux réels positifs ou nuls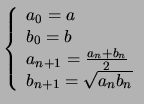
Propriétés
- La suite
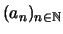 est décroissante à partir du rang
est décroissante à partir du rang 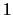 .
.
- La suite
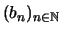 est croissante à partir du rang
est croissante à partir du rang 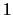 .
.
-
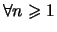 on a :
on a :
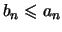 .
.
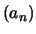 et
et 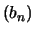 convergent vers un même réel qu'on notera
convergent vers un même réel qu'on notera 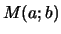 .
.
Remarque : si
Preuve :
Montrons le (3) :
Comme pour tout réel
Donc
Du (3) on déduit que
c'est-à-dire
et
Montrons le (4) :
On a ainsi
En faisant tendre
Donc
Preuve :
Un calcul simple donne :
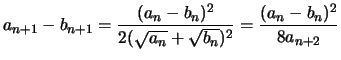
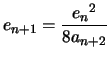
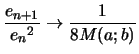
Numériquement si
Propriétés de la limite 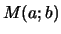
-
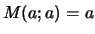 .
.
-
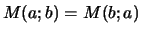 .
.
- Quel que soit
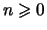
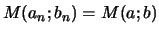 avec les mêmes notations.
avec les mêmes notations.
- Quel que soit le réel
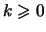
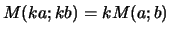 .
.
-
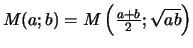 .
.
- Quel que soit
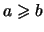
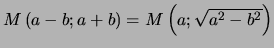 .
.
Preuve : laissée au lecteur.
Etude de la fonction
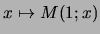
Continuité de
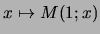
Considérons les suites de fonctions définies par récurrence pour
![]() :
:
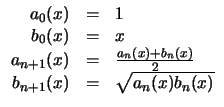
Notons pour la suite
Intéressons-nous plutôt à la propriété de cette section :
Preuve :
Travaillons sur l'intervalle compact
![]() où
où ![]() est fixé.
est fixé.
Définissons la suite de fonctions ![]() par
par
![]() .
. ![]() est continue et
la suite
est continue et
la suite ![]() est décroissante, convergeant simplement vers 0. D'après le théorème
de Dini, on sait donc
est décroissante, convergeant simplement vers 0. D'après le théorème
de Dini, on sait donc ![]() converge uniformément vers 0 sur le compact
converge uniformément vers 0 sur le compact
![]() .
.
Et comme
![]() on peut donc dire que
on peut donc dire que ![]() converge uniformément vers
converge uniformément vers ![]() sur
sur
![]() .
. ![]() étant continue,
étant continue, ![]() l'est aussi sur
l'est aussi sur
![]() , donc sur
, donc sur
![]() étant
donné que
étant
donné que ![]() était arbitraire.
était arbitraire.
Dérivabilité de
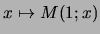
Pour étudier la dérivabilite de Définissons la fonction
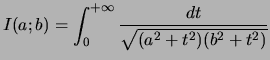
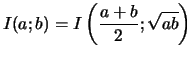
Preuve : Remarquons que :
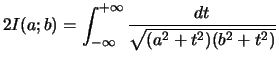
Notons :
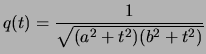
Posons :
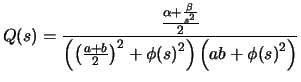
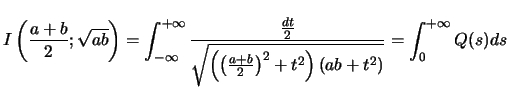
Or
De même
Or si on fait le changement de variable
Preuve :
en effet fixons ![]() , alors pour
, alors pour
![]() et
et
![]() on a :
on a :
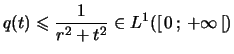
De même
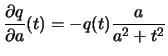
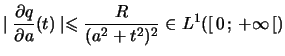
- Pour tout réel
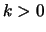 ,
,
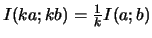 .
.
-
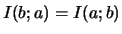 .
.
-
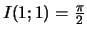 .
.
Preuve : On a vu (proposition précédente) que
![]() et
et
![]() on avait
on avait
![]()
et donc
Définissons la fonction ![]() sur
sur
![]()
Etude de
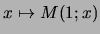 au voisinage de 0 et
au voisinage de 0 et 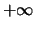
-
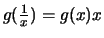 .
.
-
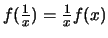 .
.
-
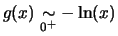 .
.
-
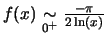
-
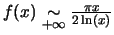
Passons au troisième et écrivons :
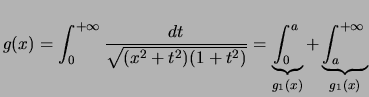
Pour
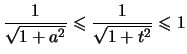
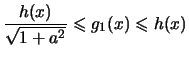
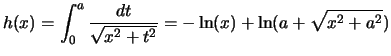
De plus
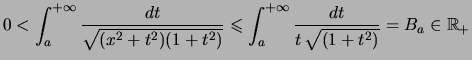
et ainsi
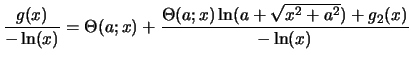
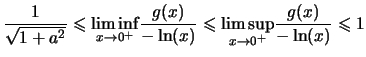
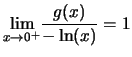
Pour
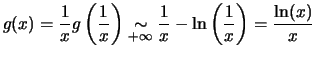
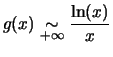
Ensuite sachant que
![]() , on trouve les deux derniers points.
, on trouve les deux derniers points.
Une équation différentielle vérifiée par
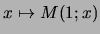 sur
sur
![$ ] 0 ; 1 [$](images/pi_agm/img187.png)
Pour tout la suite de l'exposé, on se resteindra à l'intervalle
![]() .
.
Définissons les suites de fonctions
![]() et
et
![]() par :
par :
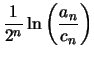 |
-
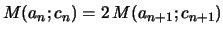 .
.
-
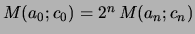 .
.
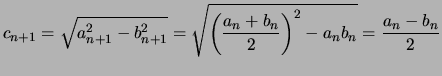
![$\displaystyle d_n(x) \xrightarrow[n \rightarrow +\infty]{} \frac{\pi}{2}\frac{f(x)}{f(\sqrt{1-x^2})}$](images/pi_agm/img201.png) (convergence simple)
(convergence simple)donc d'après le comportement de
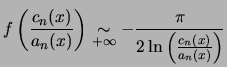
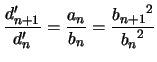
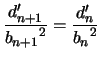
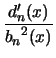 |
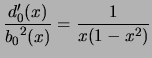 |
||
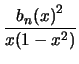 sur sur |
Preuve de la propriété : on calcule ![]() :
:
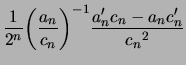 |
|||
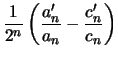 |
|||
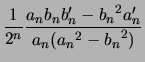 |
on calcule de même
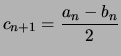
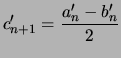
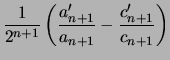 |
|||
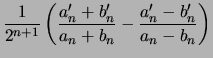 |
|||
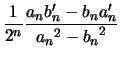 |
Donc on déduit
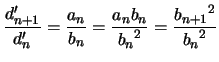
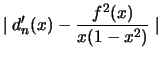 |
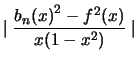 |
||
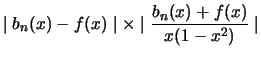 |
|||
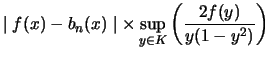 |
Résumons :
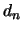 converge simplment vers
converge simplment vers
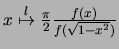
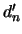 converge uniformément vers
converge uniformément vers
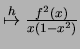 sur tout compact
de
sur tout compact
de ![$ ]0;1[$](images/pi_agm/img232.png) .
.
En dérivant
En évaluant l'équation en
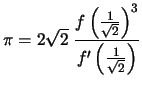
Au début de ce papier on a remarqué qu'on peut calculer avec grande précision et rapidement
![]() et on sait calculer aussi rapidement
et on sait calculer aussi rapidement ![]() (voir la méthode
de Newton).
(voir la méthode
de Newton).
Maintenant le problème qui se pose est le suivant : peut-on approcher
![]() par une suite ayant une convergence quadratique comme les deux nombres précédents ?
par une suite ayant une convergence quadratique comme les deux nombres précédents ?
Par chance, les suites dérivées ![]() et
et ![]() ont cette propriété.
ont cette propriété.
Justification des algorithmes à convergence quadratique
Etude des suites 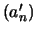 et
et 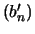 sur
sur ![$ ]0;1[$](images/pi_agm/img232.png)
Rappelons les définitions :
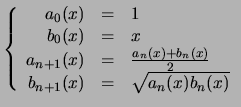
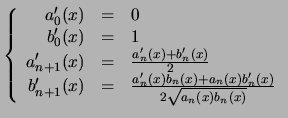
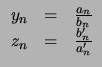
-
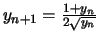 ,
,
-
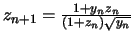 ,
,
-
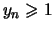 ,
,
-
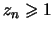 ,
,
-
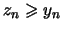 ,
,
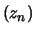 est une suite décroissante.
est une suite décroissante.
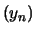 et
et 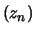 convergent uniformément sur tout compact de
convergent uniformément sur tout compact de ![$ ]0;1[$](images/pi_agm/img232.png) vers
vers 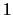 .
.
Preuve : les deux premiers points résultent des relations de récurrence précédentes
entre ![]() ,
, ![]() et
et ![]() ,
, ![]() .
.
nous savons déjà que
![]() d'où
d'où
![]() .
.
Remarquons ensuite que
![]() donc
donc
![]() sur
sur ![]() .
.
Définissons la fonction ![]() par
par
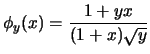
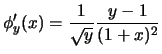
La monotonie de ![]() se déduit facilement :
se déduit facilement :
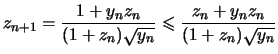
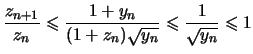
Nous avons
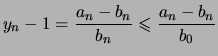
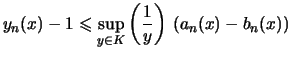
Pour tout réel ![]() de l'intervalle
de l'intervalle ![]() ,
, ![]() est une suite décroissante minorée par
est une suite décroissante minorée par ![]() donc elle converge et comme
donc elle converge et comme
![]() , on déduit de l'expression
de récurrence
, on déduit de l'expression
de récurrence
![]() que
que ![]() tend vers
tend vers ![]() .
.
Ensuite les fonctions ![]() étant continues comme
étant continues comme
![]() et la suite
et la suite ![]() étant décroissante,
on conclut grâce au théorème de Dini
que
étant décroissante,
on conclut grâce au théorème de Dini
que ![]() converge en fait uniformément sur tout compact de
converge en fait uniformément sur tout compact de ![]() vers 1.
vers 1.
et pour une fonction sur un compact
Définissons
![]()
Commençons par prouver que ![]() est bornée pour la norme
est bornée pour la norme
![]() .
.
Puisque
![]() , on a
, on a
![]() .
.
Etudions la suite ![]() .
.
On peut écrire
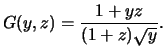
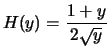
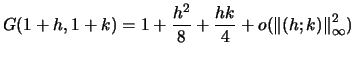
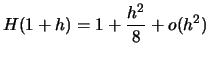
Comme
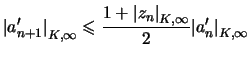
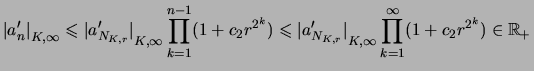
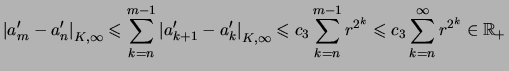
Et de la relation
Enfin puisque
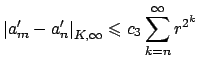
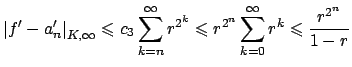
Retour sur le dernier algorithme des frères Borwein
Explication détaillée
Rapellons les suites :
Si
![]() ,
,
![]() et
et
![]()
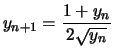
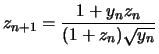
![$\displaystyle f_{n+1} = f_{n} \frac{1+y_n}{1+z_n} \xrightarrow[n \to \infty]{} \pi
$](images/pi_agm/img339.png)
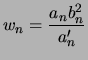
![$\displaystyle w_n(\frac{1}{\sqrt{2}}) \xrightarrow[n \to \infty]{} \frac{\pi}{2\sqrt{2}} $](images/pi_agm/img344.png)
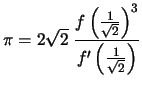
Or un calcul montre que
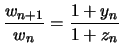
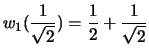
et en définissant
Premier algorithme
Explication du premier algorithme des frères Borwein
Rapellons les suites :si
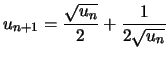
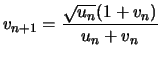
![$\displaystyle p_{n+1} = p_n u_n \frac{1+u_n}{1+v_n} \xrightarrow[n \to \infty]{} \pi
$](images/pi_agm/img48.png)
Retour sur le dernier algorithme Brent et Salamin
Explication détaillée
Ils ont découvert cet algorithme en même temps et indépendamment.Rapellons les suites :
si
alors
![$\displaystyle U_n = \frac{4a_n^2}{1-2 \sum\limits_{k=1}^{n}{2^k (a_k^2 - b_k^2 )}}
\xrightarrow[n \to \infty]{} \pi
$](images/pi_agm/img42.png)
comme vous l'avez remarqué, les suites numériques
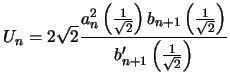
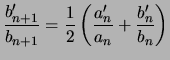
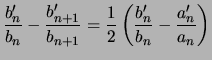
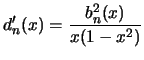
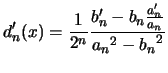
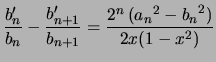
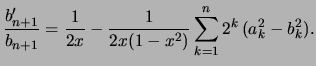
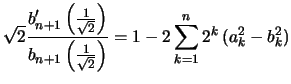
![$\displaystyle U_n = \frac{4a_n^2\left(\frac{1}{\sqrt{2}}\right)}{1-2 \sum\limit...
...t)}
{b_{n+1}'\left(\frac{1}{\sqrt{2}}\right)}
\xrightarrow[n \to \infty]{} \pi
$](images/pi_agm/img363.png)
Premier algorithme
On écrit :
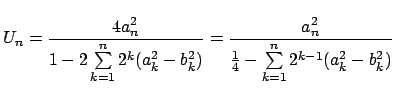
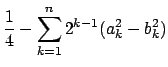 |
On obtient :
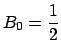
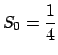
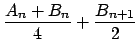 |
|||
ce qui donne l'algorithme :
|
|
|
|
|
|
| répéter pour |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| fin de la boucle | |
|
|
|
| afficher
|
Deuxime algorithme
Cette amélioration est dûe à Arnold Schönhage en 1994.Elle évite une multiplication (ce qui demande beaucoup de calcul) pour un carré (ce qui en demande moins). Puisque
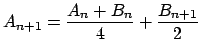
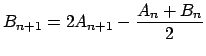
Voici l'algorithme :
|
|
|
|
|
|
| répéter pour |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| fin de la boucle | |
|
|
|
|
|
|
| afficher
|
About this document ...
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 1 pi_AGM.tex
The translation was initiated by raphi on 2004-05-30
raphi 2004-05-30